What is a recommender system?

- The recommender system produces a list of recommendations such as movies to see, products to buy, news to read, and so on.
Different Categories of Recommender Systems
-
Recommender systems can be divided into two main types: Content-based and Collaborative filter recommender systems.
-
Before plunging into the various concepts, let's show the relationship among different recommender systems.
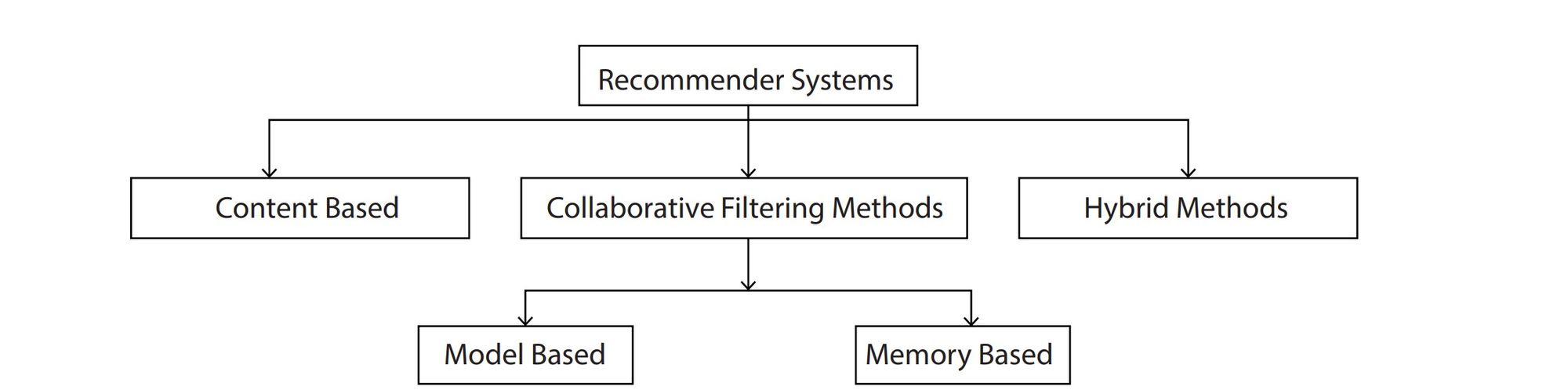
- Content-Based Recommender System
-
A content-based recommender system builds a user profile based upon the previously rated items by the user. For example, a kindle user might give a five-star rating to a book if he really likes it. Similarly, a news-reader will finish reading an item of news if he really concerns about it. These kinds of processes may signify users' interest.
-
Content-based recommender systems acquire the recommendation idea from the past data of a user based on what items a user purchased, ranked, or paid attention to.
-
Let's take a news recommender for example. News has features like categories (Politics, Finance, Sports, Entertainments, etc.) or location (local, national, or international). Some Natural Language Processing techniques such as TF-IDF scores can be used to extract such features and feed them into recommender learners.
-
In this approach, the profile of each user as well as each item is created and vectors are created to represent them.
- Item vector: A vector contains value 1 for words having high TF-IDF and 0 others.
- User vector: A vector contains the user's numerical features.
-
Finally, we build a model, based on the Item vector and User vector, that explains the observed user-item interactions.
- Collaborative Filtering Method
-
Collaborative filtering uses the feedback of other users to recommend items. These systems evaluate the quality of an item based on peer review.
-
Collaborative filtering recommender systems are based on the past interactions recorded between users and items to produce new recommendations. These interactions are stored in the so-called "user-item interactions matrix".

https://towardsdatascience.com/introduction-to-recommender-systems-6c66cf15ada
- For example, a media service company Nextflix intends to develop a recommender system based on users' historical ratings of movies. A user-item interactions matrix can be simplified as follows:
| Movie | The Godfather | Gone with the Wind | Green Book | The Big Short | Soul |
|---|---|---|---|---|---|
| Steven | 5 | 1 | 4 | 4 | 2 |
| Jessica | 2 | 2 | 4 | 2 | 5 |
| Tom | 5 | 4 | 4 | 5 | 1 |
| Beatrice | 4 | 4 | 5 | 5 | 3 |
- There are two categories of collaborative filtering RS:
- Memory-based approach:
- Users and items are represented directly by their past interaction (large sparse vectors)
- Similarity (measured by cosine similarity, Pearson's correlation, Euclidean distance, etc.) is the main concern to produce a recommendation list.
- Model-based approach
- New presentations of users and items are build based on a model (usually based on some dimension reduction techniques, such as PCA, matrix factorization, factor analysis, etc.)
- Using models (regression, neural nets, etc.) to find user ratings of unrated items.
- Memory-based approach:
0. Some Technical Details
0.1. Similarity Measures
- Cosine similarity:
\[Cos(x, y)=\frac{\sum_{i=1}^{n} x_{i} y_{i}}{\sqrt{\sum_{i=1}^{n} x_{i}^{2}} \sqrt{\sum_{i=1}^{n} y_{i}^{2}}}\]
- Jaccard Similarity:
\[J(X, Y)=\frac{|X \cap Y|}{|X \cup Y|}\]
- Pearson's Correlation:
\[\rho = \frac{\sum\left(r_{ui} - \bar{r}_{u}\right) \left(r_{vi}-\bar{r}_{v}\right)}{\sqrt{\sum \left(r_{ui}-\bar{r}_{u}\right)}\sqrt{\sum \left(r_{vi}-\bar{r}_{v}\right)}}\]
- Euclidean Distance
\[ d(X, Y)=\sqrt{\sum_{i=1}^{n}\left(x_{i}-y_{i}\right)^{2}}\]
- Manhattan Distance
\[d(X, Y)=\sum_{i=1}^{n}\left|\left(x_{i }-y_{i }\right)\right|\]
- Minkowski Distance
\[D(X, Y)=\left(\sum_{i=1}^{n}\left|x_{i}-y_{i}\right|^{p}\right)^{\frac{1}{p}}\]
0.2. Collaborative Filtering Algorithm
- Assume that we use a linear regression model to predict user's rating as follows:
\[y^{(i, j)} = (\theta ^ {(j)})^{T} x ^{(i)} + u^{i, j}\]
where \(y^{(i,j)}\) represents the rating of user j giving on item i, \(x^{(i)}\) is the feature vector of item i, and \(\theta^{(j)}\) represents the weight vector of user j.
- In this case, the collaborative filtering algorithm can be summarized in 3 steps:
- Initialize \(x ^{(1)}, \ldots, x ^{(n_{m})}\) and \(\theta ^ {(1)}, \ldots, \theta ^ {(n_{u})}\) to small random values.
- Minimize
\[ J(x ^{(1)}, \ldots, x ^{(n_{m})}, \theta ^ {(1)}, \ldots, \theta ^ {(n_{u})}) = \frac{1}{2} \sum_{(i,j): r(i,j)=1} ((\theta^{(j)})^{T} x ^{(i)})^{2} + \frac{\lambda}{2}\sum_{i=1} ^{n_{m}} \sum_{k=1} ^{n} (x_{k} ^{(i)}) ^{2} +\frac{\lambda}{2}\sum_{j=1} ^{n_{u}} \sum_{k=1} ^{n} (\theta_{k} ^{(j)}) ^{2}\]
using gradient descent (or an advanced optimization algorithm). E.g. for every \( j = 1, \ldots, n_{u}, i= 1, \ldots, n_{m} \):
\[ x_{k} ^{(i)} := x_{k} ^{(i)} - \alpha \left( \sum _ {j: r(i,j)=1}((\theta^{(j)})^{T} x ^{(i)} - y ^{(i, j)}) \theta_{k} ^{(j)} + \lambda x_{k} ^{(i)}\right)\]
\[ \theta_{k} ^{(j)} := \theta_{k} ^{(j)} - \alpha \left( \sum _ {j: r(i,j)=1}((\theta^{(j)})^{T} x ^{(i)} - y ^{(i, j)}) x_{k} ^{(i)} + \lambda \theta_{k} ^{(j)}\right)\]
- For a user with weight vector \(\theta\) and a movie with (learned) feature vector \(x\), predict a star rating of \(\theta ^{T} x\).
Announcement: The content above is credited to many resources. All blogs on this website are study notes, not copyright publications.