What is Isotonic Regression?
Short Answer
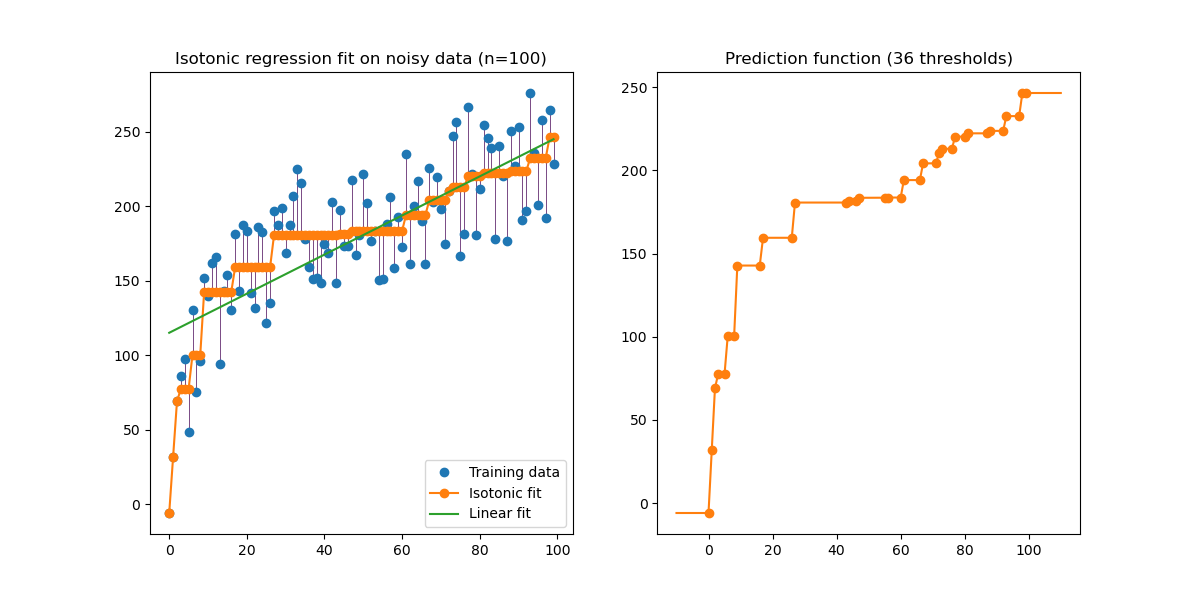
- Isotonic regression is similar to linear regression, except for some monotonic constraints. Additionally, linear regression is global, while isotonic regression is pairwise.
Long Answer
-
Assume we have dataset \(\{(x_{1}, y_{1}), (x_{2}, y_{2}), \ldots, (x_{n}, y_{n})\}\) such that \(x_{1}<x_{2}< \cdots <x_{n}\). Isotonic regression looks for \(\beta_{1}, \beta_{2}, \ldots, \beta_{n} \in \mathbb{R}\), such that the \(\beta_{i}\)'s approximate the \(y_{i}\)'s well while being monotomically non-decreasing.
-
In mathematics, the \(\beta_{i}\)'s are the solution to the optimization problem:
\[\operatorname{minimize}_ {\beta_{1}, \ldots, \beta_{n}} \sum_{i=1}^{n}\left(y_{i}-\beta_{i}\right)^{2} \]
subject to the constraint \(\beta_{1} \leq \cdots \leq \beta_{n}\).
-
Generally, we use isotonic regression when we have some preknowledge to ensure that there is a non-decreasing relationship between the predictor and response.
-
Python codes for isotonic regression:
from sklearn.isotonic import IsotonicRegression
iso_reg = IsotonicRegression().fit(X,y)
iso_reg.predict([x1, x2])