2 min read

What is Support Vector Machines (SVM)?

What is Support Vector Machines (SVM)?

  • A support-vector machine (SVM) constructs a hyperplane or set of hyperplanes in a high- or infinite-dimensional space, which can be used for classification, regression, or other tasks like outlier detection.

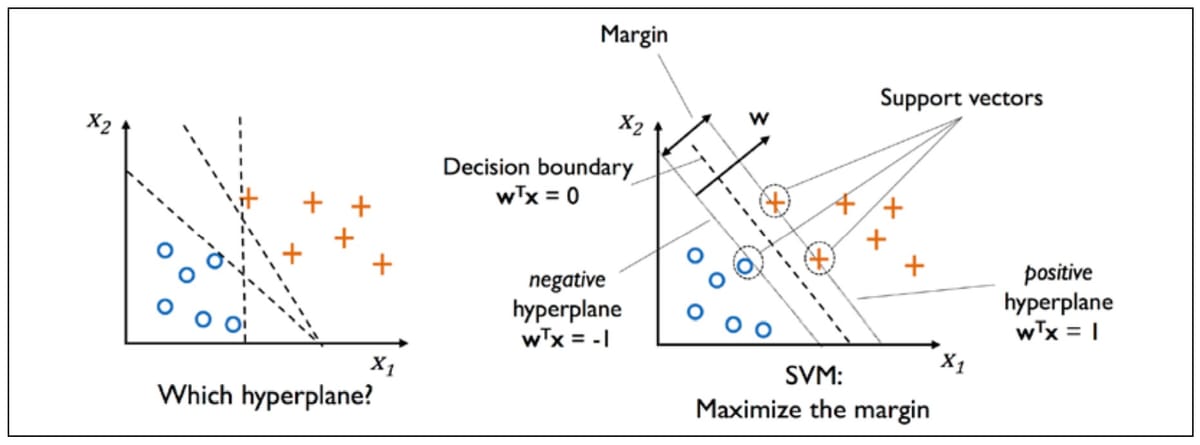
  • A good separtion is achieved by the hyperplane that has the largest distance to the nearest training-data point of any class.

svm-1

  • We are given a training dataset of \(n\) points:

\[(x_{1}, y_{1}), \ldots, (x_{n}, y_{n})\]

where the \(y_{i}\) are either 1 or -1, each indicating the class to which the point \(x_{i}\) belongs. Each \(x_{i}\) is a \(p\)-dimensional real vector.

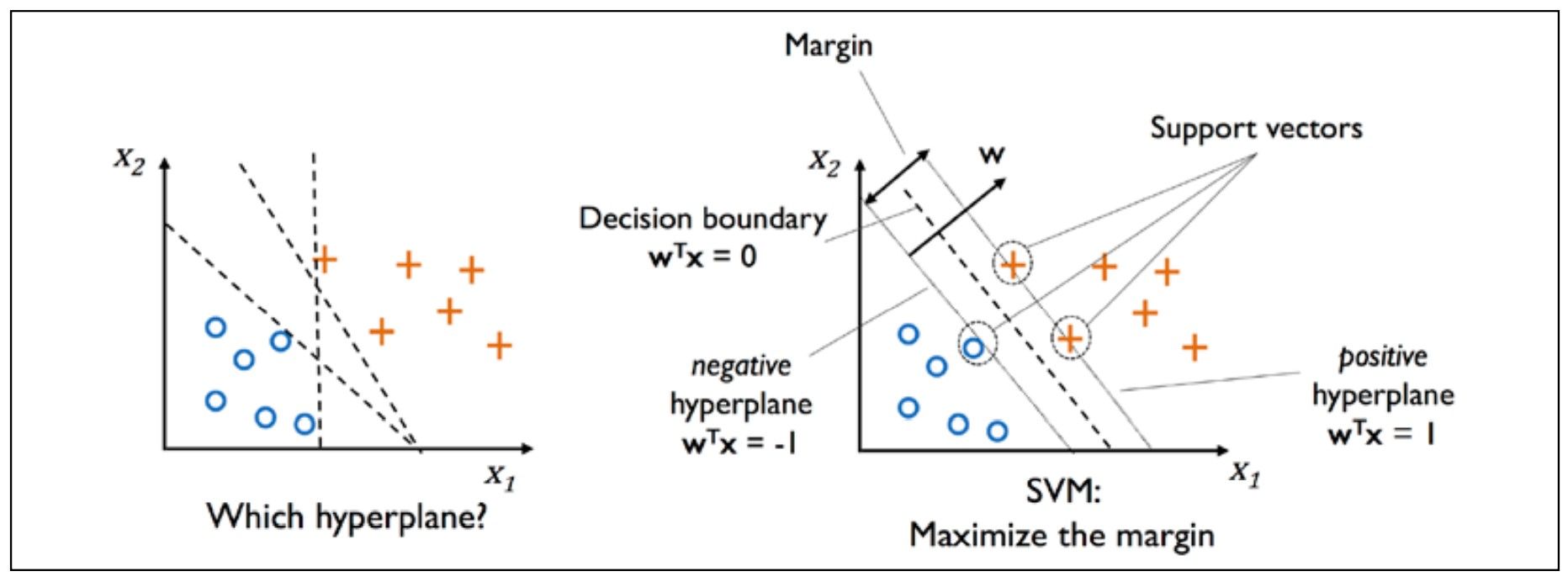
  • To find the "maximum-margin hyperplane" that divides the two different classes is equivalent to find a vector \(\boldsymbol{w}\) such that the distance between the two planes below is maximized.

\[\boldsymbol{w}^{T}\boldsymbol{x}-b = 1  \  v.s. \  \boldsymbol{w}^{T}\boldsymbol{x}-b = -1 \]

  • Geometrically, the distance between these two hyperplances is \(\frac{2}{||\boldsymbol{w}||}\), so to maximize the distance between the planes is equivalent to minimize \(||\boldsymbol{w}||\).

  • If there is no point falling into the margin, then the SVM is said to have hard-margin. In this case, we should add the following constraint: for each \(i\)

\[y_{i}(\boldsymbol{w}^{T}\boldsymbol{x}-b) >  1 \]

  • Please note that the max-margin hyperplane is completely determined by those \(x_{i}\) that lie nearest to it. These \(x_{i}\) are called support vectors.

  • To extend SVM to cases in which the data are not completely seperable, we need to introduce a slack variable \(\xi^{(i)}\) for each instance: \(\xi^{(i)}\) measures how much the \(i^{th}\) instance is allowed to violate the margin.

  • The new objective to be minimized (subject to the constraints) becomes:

\[ \frac{1}{2} ||\boldsymbol{w}||^{2} + C \left( \sum_{i} \xi^{(i)} \right)\]

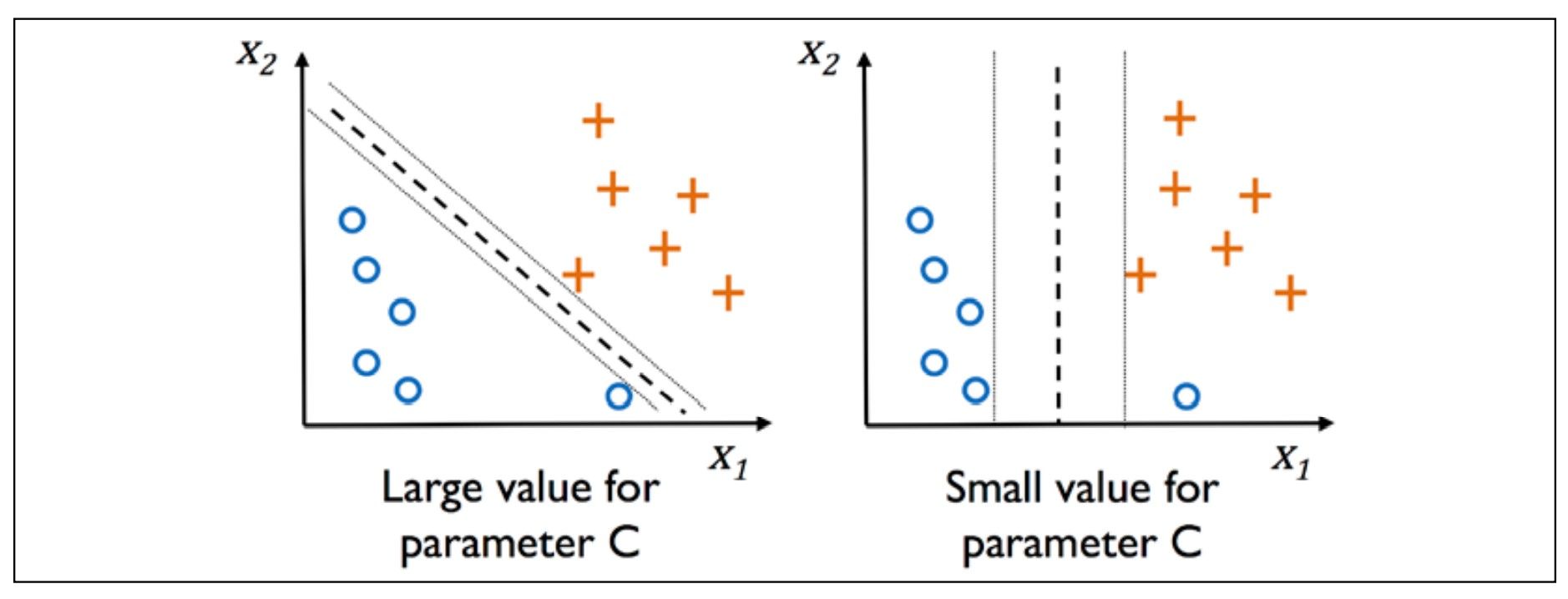
  • Via the variable, \(C\), we can then control the penalty for misclassification. Large values of \(C\) correspond to large error penalties, which means we are more intolerable about misclassification. We can then use the \(C\) parameter to control the width of the margin and therefore tune the bias-variance tradeoff, as illustrated in the following figure:

soft

  • Python code for linear SVM:
    from sklearn.svm import SVC
    svm = SVC(kernel='linear', C=1.0, random_state=1)
    svm.fit(X, y)
    svm.predict(X_test)

The main reference for this blog is Python Machine Learning written by Sebastian Raschka & Vahid Mirjalili.