2 min read

What is Expectation-Maximization (EM) Algorithm?

What is Expectation-Maximization (EM) Algorithm?

Short Answer

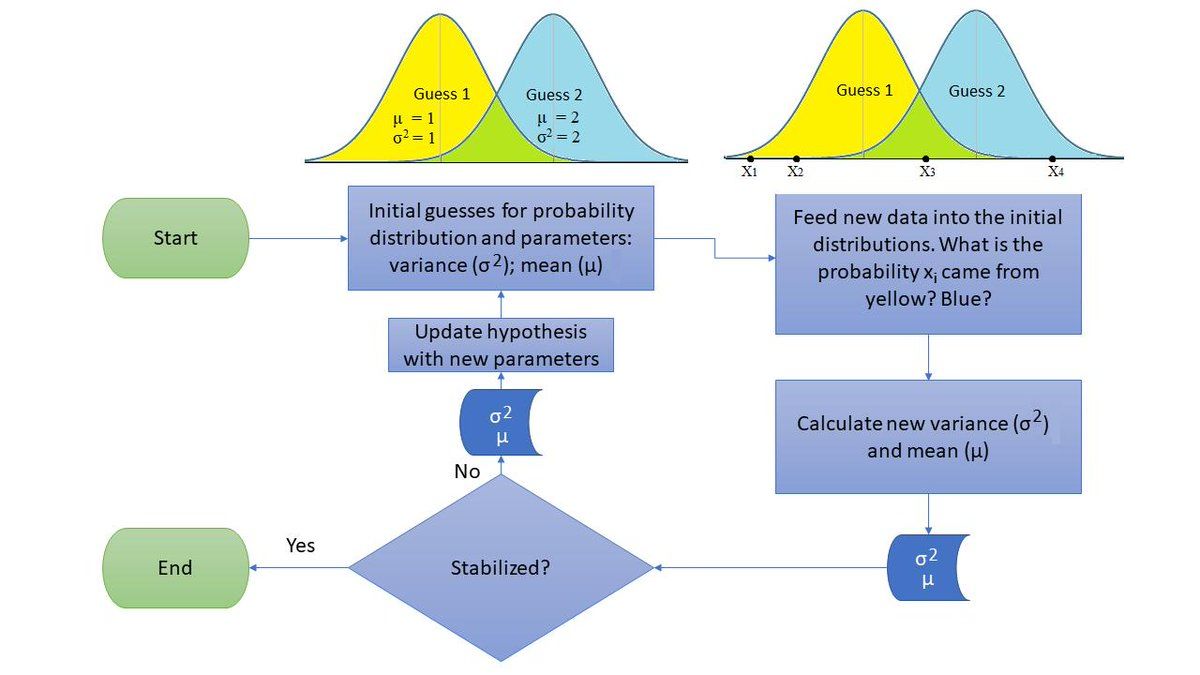
  • Expectation Maximization (EM) is an iterative algorithm for finding the maximum a posteriori (MAP) estimated of parameters in statistical modles, where the model depends on unobserved latent variables.

  • The algorithm iteratively repeats two steps until convergence or until a maximum number of iteratively repeats two steps until convergence or until a maximum number of iterations has been reached.

    • The E-step creates a function for the expectation of the log-likelihood evaluated using the current estimate of the parameter.
    • The M-step computes parameters maximizing the expected log-likelihood found on the E step.

Long Answer

  • Given the statistical model which generates a set \(\boldsymbol{X}\) of observed data, a set of unobserved latent data or missing values \(\boldsymbol{Z}\), and a vector of unknown parameters \(\boldsymbol{\theta}\), along with a likelihood function \(\boldsymbol{L} (\boldsymbol{\theta}; \boldsymbol{X}, \boldsymbol{Z}) = p (\boldsymbol{X}, \boldsymbol{Z} \mid \boldsymbol{\theta})\), the maximum likelihood estimate (MLE) of the unknown parameters is determined by maximizing the marginal likelihood of the observed data.

\[L(\boldsymbol{\theta} ; \mathbf{X})=p(\mathbf{X} \mid \boldsymbol{\theta})=\int p(\mathbf{X}, \mathbf{Z} \mid \boldsymbol{\theta}) d \mathbf{Z}=\int p(\mathbf{Z} \mid \mathbf{X}, \boldsymbol{\theta}) p(\mathbf{X} \mid \boldsymbol{\theta}) d \mathbf{Z}\]

  • However, this quantity is often intractable since \(\mathbf{Z}\) is unobserved and the distribution of \(\mathbf{Z}\) is unknown before attaining \(\mathbf{\theta}\).

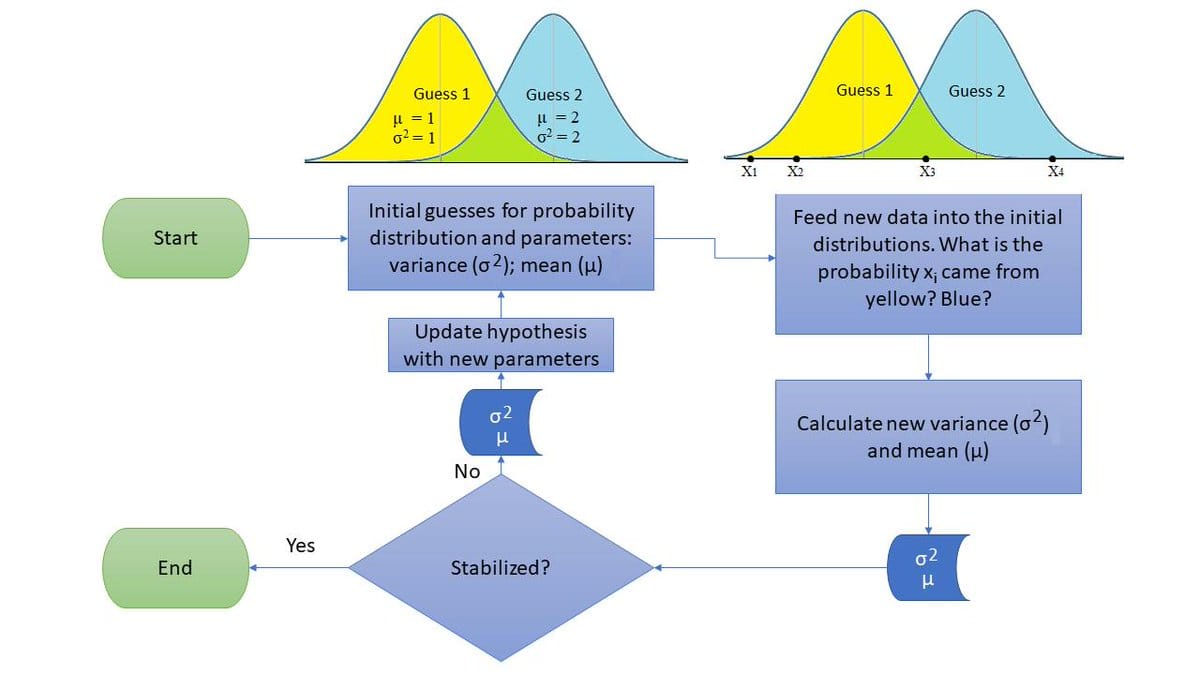
  • The EM algorithm seeks to find the MLE of the marginal likelihood by iteratively applying the following two steps:

    • Expectation step (E step): Define \(Q(\boldsymbol{\theta} \mid \boldsymbol{\theta}^{(t)})\) as the expected value of the log likelihood function of \(\mathbf{\theta}\), with respect to the current conditional distribution of \(\mathbf{Z}\) given \(\mathbf{X}\) and the current estimates of the parameters \(\boldsymbol{\theta}^{(t)}\):

\[Q(\boldsymbol{\theta} \mid \boldsymbol{\theta}^{(t)})=\mathrm{E}_{\mathbf{Z} \mid \mathbf{X}, \boldsymbol{\theta}^{(t)}}[\log L(\boldsymbol{\theta} ; \mathbf{X}, \mathbf{Z})]\]

  • Maximization step (M step): Find the parameters that maximize this quantity:

\[\boldsymbol{\theta}^{(t+1)}=\underset{\boldsymbol{\theta}}{\arg \max } Q(\boldsymbol{\theta}\mid \boldsymbol{\theta}^{(t)})\]

  • The algorithm for EM:
    1. Initialize the parameters \(\mathbf{\theta}\) to some random values.
    2. Compute the probability of each possible value of \(\mathbf{Z}\), given \(\mathbf{\theta}\).
    3. Use the just-computed values of \(\mathbf{Z}\) to compute a better estimate for the parameters \(\mathbf{\theta}\) (update \(\mathbf{\theta}\) value).
    4. Iterate steps 2 and 3 until convergence.

em-1