Activation Functions II: Rectified-based Activation Functions

Introduction

We have given a brief introduction to the basic activation functions in the previous blog. In this post, we would like to take you further into the trainable activation function world and to give the rectified-based activation functions a close-up.

After years of development, activation functions have grown into a big family. The figure below can be taken as a family portrait of them.

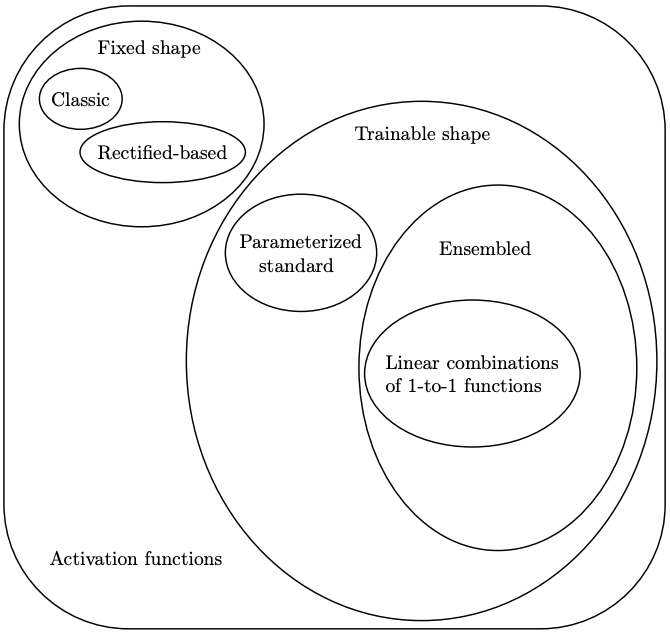
In the figure above, we can see that activation functions can be divided into two main categories:

1. Fixed-shape activation functions: all the activation functions with a fixed shape, for instance, all the classic activation functions, such as Sigmoid, Tanh, ReLU, fall into this category. However, since the introduction of rectified functions can be considered a milestone in activation function history, we would like to granulate fixed-shape activation functions further into two subcategories:

   -- classic activation function: all the functions that are not in the rectifier family, such as the Sigmoid, Tanh, and step functions.

   -- rectified-based function: all the functions belonging to the rectifier family, such as ReLU, LReLU, etc.

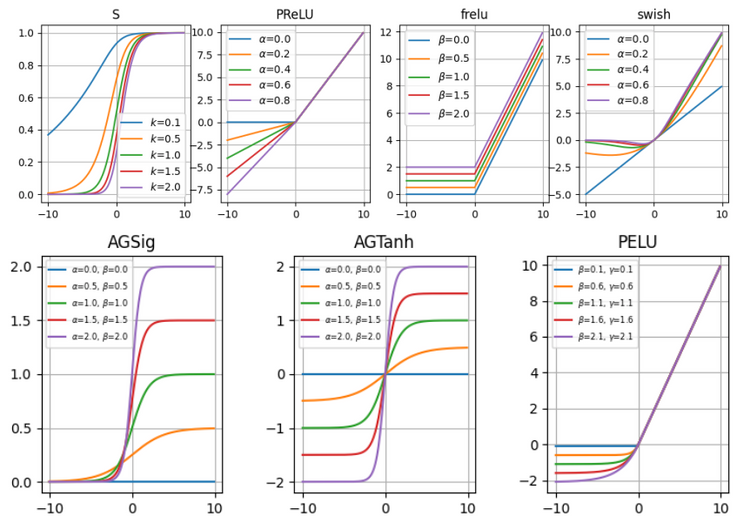
As a review, we give the expression of the most used classic activation functions in the table below.

Their function graphs are:

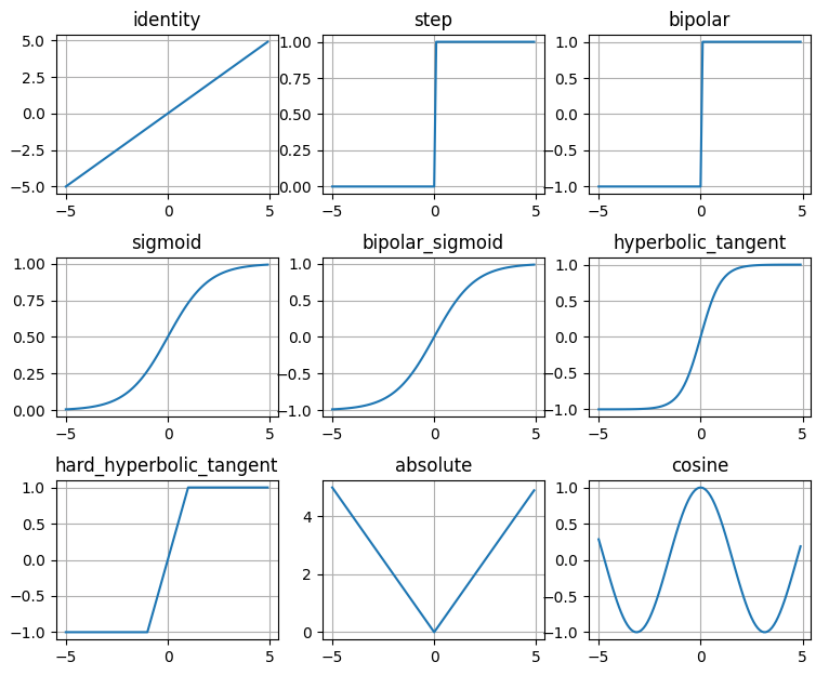
As for the rectified-based functions, we will give them more words later, so we don't plan to discuss them in detail right now.

2. Trainable activation functions: this class contains all the activation functions the shape of which is learned during the training phase. Among all the trainable activation functions described in the literature we can isolate two different families:
   -- parameterized standard functions: they are defined as a parametric version of a standard fixed function whose parameter values are learned from data.
   -- functions based on ensemble methods: they are defined by mixing several distinct functions.

Trainable activation functions will be explained in detail in the next blog. We intend to focus primarily on the rectified-based activation functions in this post.

Rectified-based Activation Functions

Rectified-based activation functions including ReLU and its relatives have been the standard de facto in current neural network architectures. Studies showed the performance improvements of networks equipped with rectifier-based activation functions.

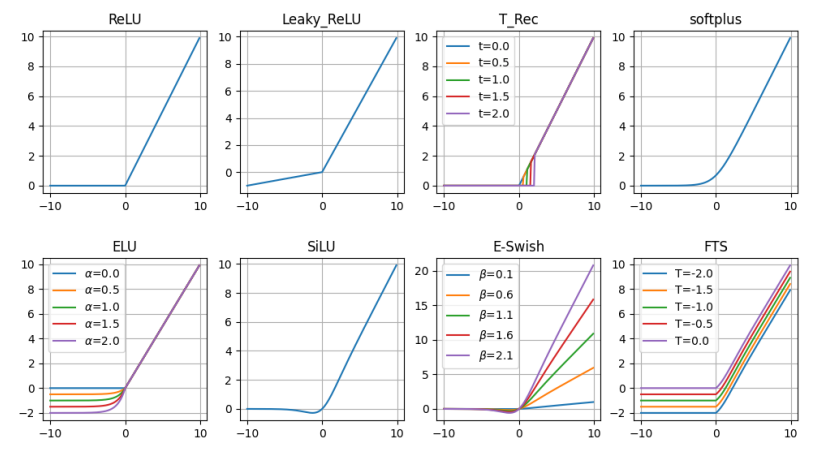
First, we would like to give you a whole picture of this family, and then we will introduce them to you one by one.

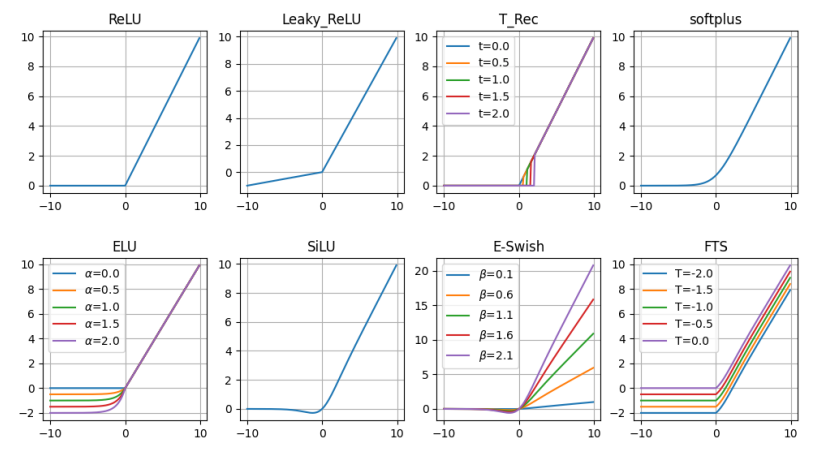
ReLU

This function has been introduced in the previous blog. It has the form $ReLU(a) = max(0, a)$, which has significant positive features:

• It alleviates the vanishing gradient problem of being not bounded in at least one direction.
• It facilitates sparse coding, as the percentage of neutrons that are really active at the same time is usually very low.

However, it also suffers from some defects, such as the "Dying ReLU" problem or the non-differentiability at zero, which has been mentioned before.

Leaky ReLU (LReLU)

One of the earliest rectified-based activation functions based on ReLU. It was invented to alleviate the potential problems of the ReLU mentioned above. It is defined as:

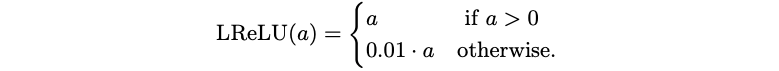
A Leaky Rectifier Activation Function allows the unit to give a small gradient when the unit is saturated and not active. However, its performance is still very similar the that of the standard rectifiers.

A randomized version (Randomized Leaky ReLU), where the wight value for $a$ is sampled by a uniform distribution $U(l, u)$ with $0 \leq l < u < 1$.

Truncated Rectified

Truncated Rectified was proposed to tackle the problem that be caused by ReLU in a particular type of DNN (Autoencoders). The Trunncated Rectified activation function can be defined as:

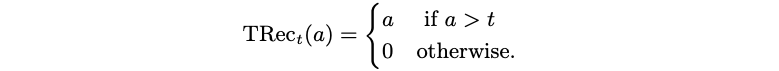
We can use TRec only during training, and then replace it with ReLU during testing, which could obtain both sparse coding and the minimizing of the error function without any kind of weight regularization.

Softplus

Softplus can be seen as a smooth approximation of ReLU function. It is defined as
$$Softplus(a) = log(1 + exp(a))$$
The smoother form and the lack of points of non-differentiation could suggest a better behavior and an easier training as an activation function. However, experimental results tend to contradict this hypothesis, suggesting that ReLU properties can help supervised training better than softplus functions.

Exponential Linear Unit (ELU)

The ELU is an activation function that keeps the identity for positive arguments but with non-zero values for negative ones. It is defined as:

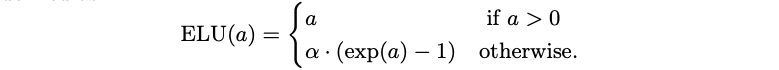
where $\alpha$ controls the value for negative inputs. The values given by ELU units push the mean of the ativations closer to zero, allowing a faster learning phase, at the cost of an extra hyper-parameter ($\alpha$) which requires to be set.

Sigmoid-weighted Linear Unit

Sigmoid-weighted Linear Unit is a sigmoid function weighted by its input:
$$SiLU(a) = a \cdot \sigma (a)$$
SiLU is differentiable, its derivative is also proposed as activation function, which can be written as:
$$dSiLU(a) = sig(a)(1 + a(1 - sig(a)))$$
Although these functions have been tested on reinforcement learning tasks. They are not widely used in practice.

E-swish

A SiLU variation is proposed by adding a multiplicative coefficient to the SiLU function, and obtain:
$$E-swish_{\beta}(a) = \beta \cdot a \cdot \sigma (a)$$
with $\beta \in \mathbb{R}$. The function name comes from the Swish activation function, a trainable version of SiLU function proposed in 2018. However, E-Swish has no trainable parameters, leaving to the user the tuning of the $\beta$ parameter.

Flatten-T Swish

Flatten-T Swish has properties of both ReLU and sigmoid, combining them in a manner similar the the Swish function.

When $T=0$ the function becomes $ReLU(a) \cdot \sigma (a)$, a function similar to Swish-1, where the ReLU function substitutes the identity. $T$ is an additional fixed threshold value to allow the function to return a negative value (if $T<0$), different from the classic ReLU function.

GELU

Gaussian Error Linear Units (GELUs) is proposed in 2020. The authors motivate their activation by combining properties from dropout, zoneout, and ReLUs. Assume that the inputs approximately follow a normal distribution, GELU can be defined as:

$$GELU(a) = a P(X \leq a) = a \Phi (a) = x \cdot \dfrac{1}{2}[ 1+ erf(x/\sqrt{2})]$$

It can be approximated with

$$a \sigma(1.702a)$$

From the approximation above, we can see that it can be approximately regarded as a ReLU family member.

We plot GELU. ReLU and ELU together below to demonstrate the similarities and differences between them.

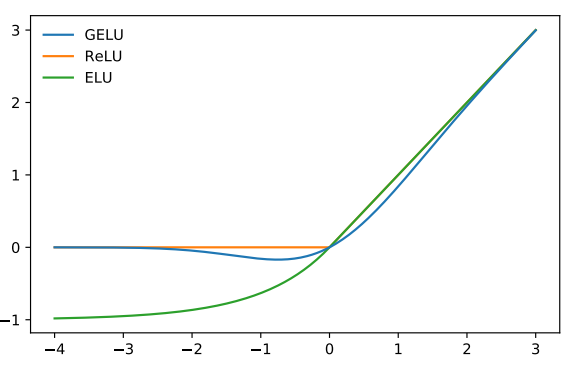
At the end of this blog, we would like to give the usage of some activation functions mentioned in this post to give you a general impression of their popularity.

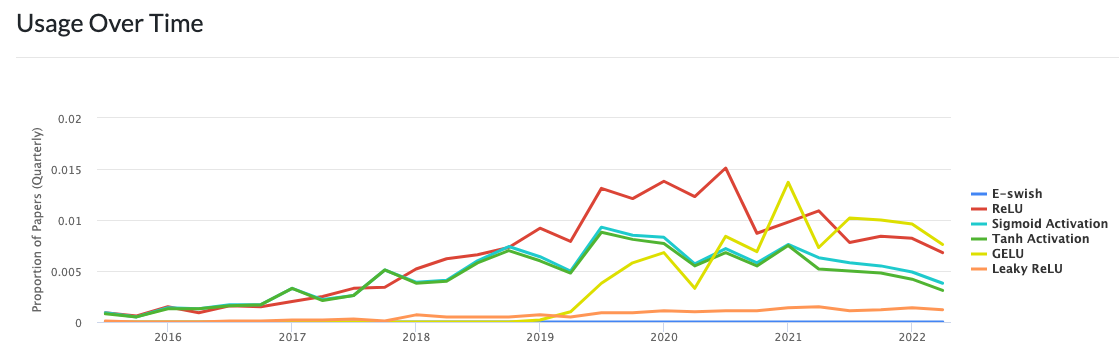
We can see that the usage of GELUs has grown subtantially over the past couple of years. Whether it could remain the dominant activation function in the next few years, we will wait and see.

Reference:

1. A Survey on Modern Trainable Action Functions, Andrea Apicella et al.
2. E-swish: Adjusting Activations to Different Network Depths, Eric Alcaide.
3. Gaussian Error Linear Units (GELUs), Dan Hendrycks, Kevin Gimpel.